Lo studio seguente mostra come situazioni apparentemente slegate
hanno invece una logica comune:
un fenomeno resta inspiegabile finché il
campo di osservazione non è abbastanza ampio da includere il contesto in
cui il fenomeno si verifica.
Se l'osservatore non si rende conto dell'intreccio di relazioni tra un evento e la matrice in cui esso si verifica, tra un organismo e il suo ambiente, o è posto di fronte a qualcosa dí "misterioso" oppure è indotto ad attribuire al suo oggetto di studio certe proprietà che l'oggetto può non avere.
Le relazioni (o più in generale le corrispondenze) tra enti costituiscono così un efficace e forse indispensabile strumento metodologico di indagine per la comprensione di manifestazioni di ogni genere, siano esse fenomeni di tipo sociale, economico o fisico, oppure meccanismi causali, o anche tipologie organizzative (strutture).
Da tutto ciò deriva l'importanza e la necessità di una "teoria delle corrispondenze" o, più esattamente, di una "teoria matematica delle corrispondenze", poiché è tipico della matematica che le relazioni tra gli enti (e non la loro natura) siano l'oggetto d'interesse più immediato.
fenomeni di tipo sociale, economico o fisico, oppure meccanismi causali, o anche tipologie organizzative (strutture).
Da ciò deriva l'importanza e la necessità di una "teoria matematica delle corrispondenze", poiché è tipico della matematica che le relazioni tra gli enti (e non la loro natura) siano l'oggetto d'interesse più immediato.
Questa lezione costituisce una introduzione alla teoria matematica delle corrispondenze.
Tratteremo i seguenti punti:
- Il concetto di corrispondenza: (rappresentazione e classificazione)
- Le funzioni: (iniettività, surgettività e biettività)
- Le funzioni reali elementari.
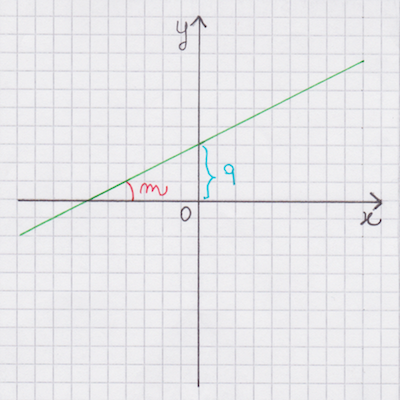
LA FUNZIONE LINEARE.
Si partirà dall'esame di problemi esprimibili graficamente mediante una funzione lineare della quale poi studieremo tutte le caratteristiche.
Un esempio di funzione lineare lo si trova in matematica finanziaria studiando i movimenti di capitale nel tempo e gli interessi che esso produce.
Questo problema è esprimibile mediante una funzione di tipo lineare;
infatti, al crescere del tempo, l'interesse aumenta nello stesso modo: dopo un anno si avrà un certo interesse, dopo tre anni l'interesse sarà triplicato.
Questo é tipico della proporzionalità diretta, la cui rappresentazione grafica é data da una retta.
Rappresentare graficamente un problema, trovando un legame tra due variabili, che per ora ipotizziamo di tipo lineare, è utile sia per visualizzare la situazione, ma anche per ricavare ulteriori informazioni e quindi per studiare e analizzare fenomeni di diversa natura.
y = ax2 + bx + c con a, b, c ∈ R, ma a≠0
Se b e c sono ambedue uguali a 0, l'equazione assume la forma:
y = ax2
che è detta funzione quadratica o legge di proporzionalità quadratica.
Un esempio di funzione quadratica lo si ricava studiando la caduta di un corpo sotto l'azione della forza di gravità:
Lo spazio s percorso dal corpo che cade dipende dal tempo t trascorso secondo la legge:
s=g/2•t2
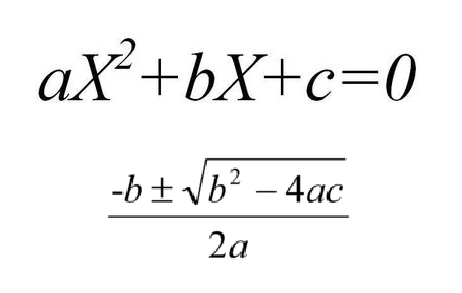
Analizzeremo i metodi di risoluzione dei sistemi di equazioni di primo e di secondo grado, che ci permettono di determinare i punti di intersezione tra le curve le cui equazioni formano il sistema, e i sistemi di disequazioni di primo e di secondo grado in una variabile, che ci permettono di risolvere le disequazioni fratte e quindi di studiare il segno di una funzione fratta.
I sistemi di formule sono spesso il modello matematico più adatto per risolvere problemi o situazioni reali.
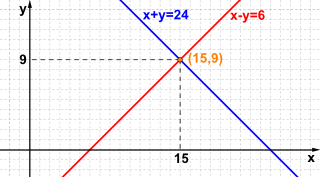
è quello di costruire una tabella di valori che esplicita il legame tra la variabile indipendente x e la variabile dipendente y.
Rappresentando le coppie (x, f(x)) come punti in un piano cartesiano, ricaviamo una descrizione necessariamente discreta del grafico della funzione.
Tale metodo, evidentemente, può risultare soddisfacente per funzioni definite su un insieme discreto, ma è decisamente inadatto a rappresentare funzioni definite su un insieme continuo.
Per queste ultime sarà necessario individuare procedure alternative capaci di fornire informazioni non solo puntuali sull'andamento di una funzione, ma anche "globali".
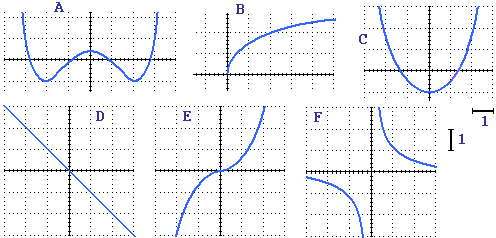
Risulta spesso utile riconoscere se il grafico cercato sia ottenibile sottoponendo
GRAFICI DI FUNZIONI NOTE a PRECISE TRASFORMAZIONI GEOMETRICHE (simmetrie, traslazioni, omotetie, ecc.).
Ed è quanto verrà esaminato in questa lezione, unitamente alle tecniche operative di trasformazione.
Una funzione y = f(x) si dice periodica se per ogni numero reale x esiste un numero T∈ R tale che si abbia:
f(x+kT) = f(x) con k∈ Z
Il numero T è detto periodo della funzione.
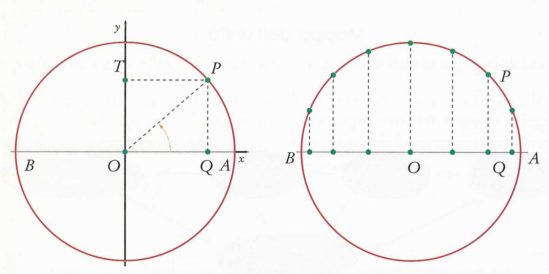
Un fenomeno fisico descritto da una funzione periodica è, ad esempio, il moto armonico, proiezione su un diametro di un moto circolare uniforme.
Mentre il punto P si muove sulla circonferenza con velocità costante, il punto Q, proiezione di P sul diametro AB, si muove di moto armonico:
mentre il punto P percorre archi uguali in tempi uguali, la sua proiezione Q percorre spazi disuguali. Il moto di un pendolo o di un peso attaccato ad una molla, in determinate condizioni, sono moti armonici. Per descrivere questi moti, come per descrivere alcuni fenomeni di acustica, di elettromagnetismo, di ottica, SI UTILIZZANO LE FUNZIONI GONIOMETRICHE, i modelli matematici che più si prestano a descrivere e studiare i fenomeni di natura periodica.
Tali formule restano comunque valide sia da un punto di vista teorico, sia per poter riscrivere in forma equivalente equazioni o disequazioni e renderle quindi riconducibili a casi noti e come tali immediatamente risolubili.
Cercheremo di:
- Riconoscere che una funzione goniometrica non soddisfa la legge lineare f(x1+x2) = f(x1) + f(x2).
- Conoscere le formule che consentono di ridurre la complessità di una espressione goniometrica.
- Acquisire ulteriore capacità nell'effettuare dimostrazioni di carattere sia algebrico che geometrico.
- Utilizzare le tecniche algebriche e grafiche per risolvere equazioni e disequazioni goniometriche.
Lo studio razionale di tali strutture porta a scoprire nuove relazioni tra le grandezze.
Queste, opportunamente interpretate, forniscono spesso informazioni significative per la conoscenza del fenomeno.
Ed è possibile che fenomeni diversi si traducano in uno stesso modello matematico.
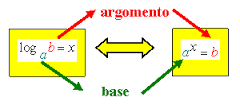
Svolgeremo lo studio delle proprietà della funzione esponenziale: (y = kax)
e della sua inversa, la funzione logaritmica: (y = logax)
che ha avuto un ruolo particolarmente importante nella storia del calcolo.